PyNOT : wave2d

This task will take a science image and apply a transformation to remove image distortions along the spatial axis. These distortions are most visible in the associated arc line image where the emission lines of the calibration lamp show up as curved lines instead of straight lines. The task wave2d performs the following sub-tasks:

Image edge detection

The first step in the process is to detect the edges of the exposed region of the image. This is done by finding the location along the slit where the arc lines are no longer visible. This is illustrated in Fig. 1, where the significant curvature of the arc lines is visible as well. The edge detection is controlled by the single parameter edge_kappa. This parameter determines the significance level above which the emission lines must be detected. If the emission lines are very weak at the edge, it might be necessary to lower this threshold in order to detect the fainter edges. Setting this parameter too high might result in an aggressive rejection of all emission lines, and hence a very unstable edge detection.

Note that for images where only the central part of the CCD has been read out, this step is not technically necessary but it allows the user to identify cases where the arc lamp illumination failed during the calibration exposure, or other glitches.

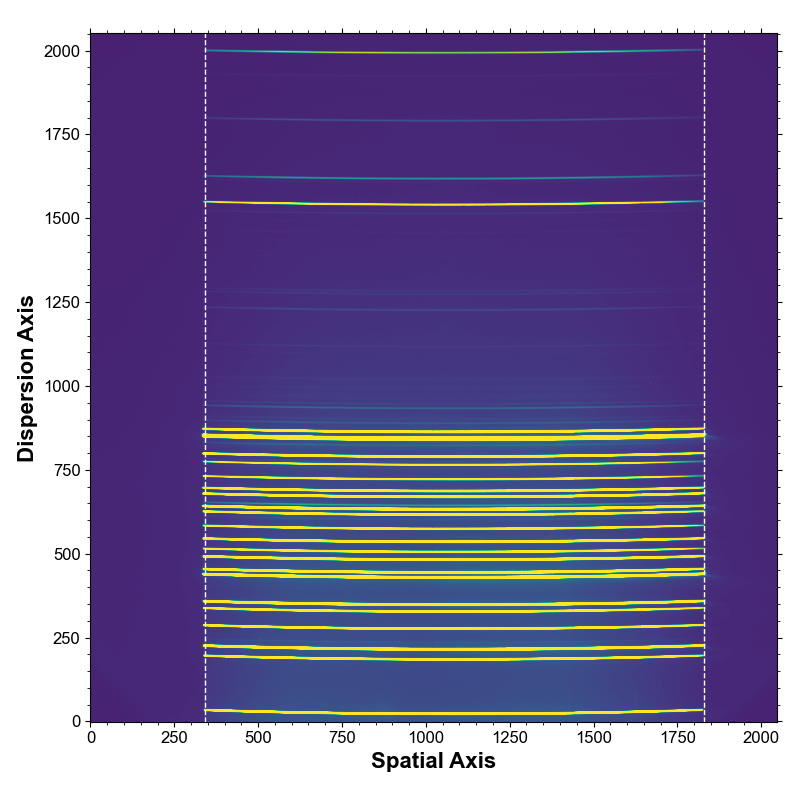
Fig. 1 – Bias and overscan subtracted arc lamp image. The white dashed lines mark the edges of the exposed area on the CCD.

The arc and science images are then trimmed and rotated to have dispersion along the horizontal axis. This is done to speed up the calculations, as operations on rows in Python are slightly faster than operations by columns. The resulting trimmed arc image is shown in Fig. 2 together with examples of spectra along three rows (one at either end and one in the middle).

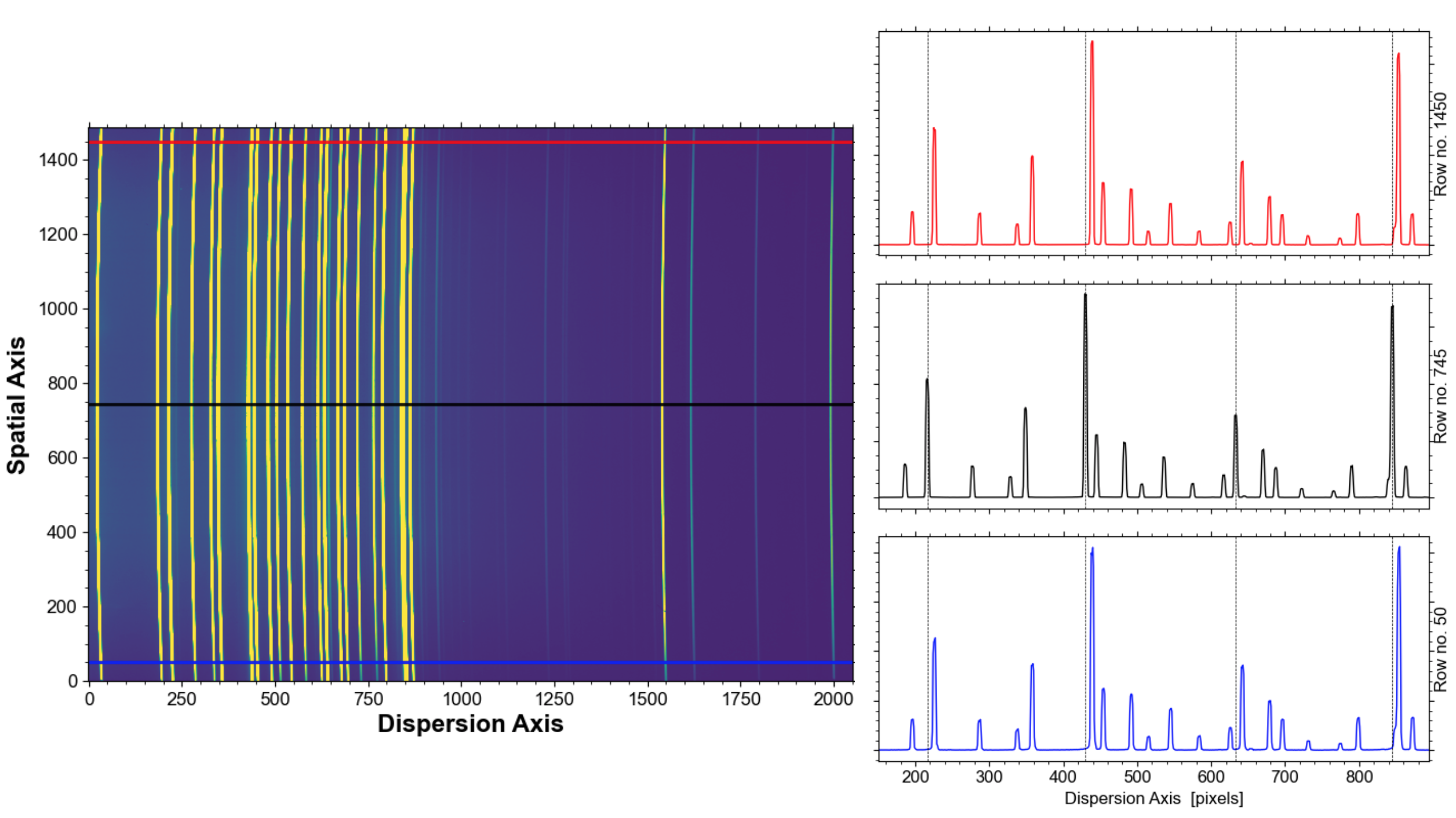
Fig. 2 – Trimmed and rotated arc line image (left) with three spectra from different rows (right). The red, black and blue spectra correspond to the three colored slices along rows in the 2D image on the left. A few emission lines have been identified in the central spectrum and their positions along the dispersion axis are projected to the other plots (as dotted lines). This clearly illustrated the curvature leading to offsets in wavelength as function of image columns.

Arc lamp continuum subtraction

Now that the arc line image has been trimmed, we can start to fit the positions of the emission lines for each spatial row. But before the emission lines are fitted, the smoothly varying lamp continuum is subtracted in order not to bias the measurements of the line positions. The lamp continuum is estimated for each row by masking out the emission lines using a median-filtering procedure. The resulting continuum regions are then interpolated using a Chebyshev polynomial of order given by the parameter order_bg. Lastly, the continuum estimate is subtracted from the given row.

Arc line fitting : the 2D pixel table

For each arc line identified by PyNOT-identify the task now fits the location of the given emission line for each spatial row. This is illustrated in Fig. 3 for one emission line. The line center is obtained by fitting a Gaussian to the predicted position from the input pixel table (given by the required argument table). The fit is performed in a small region around each line, by default a region of 10 pixels on either side is used. This region can be controlled by the parameter fit_window.

Note: if many of the identified arc lines are close together (i.e., within the fit_window) the fit may fail silently since the stronger of the emission lines will always be fitted. This leads to degeneracies in the subsequent calculation of the wavelength grid. One way to see this, is if the wavelength residuals are very large. In some cases the code will fail with an error that the wavelength solution is not monotonic. This is most likely a result of arc line identifications that are too closely spaced or a fit_window that is too wide.
The fit_window must, however, be wide enough such that the maximum curvature of the arc line falls within the fitting region. The 'maximum curvature' is printed in the log after the fitting.

The fitted positions are then median filtered and fitted by a Chebyshev polynomium as a function of the spatial pixel value (top right panel of Fig. 3). The polynomial order used is controlled by the parameter order_2d. The fitted polynomium is then used to calculate the predicted position for each spatial row (red line in Fig. 3).

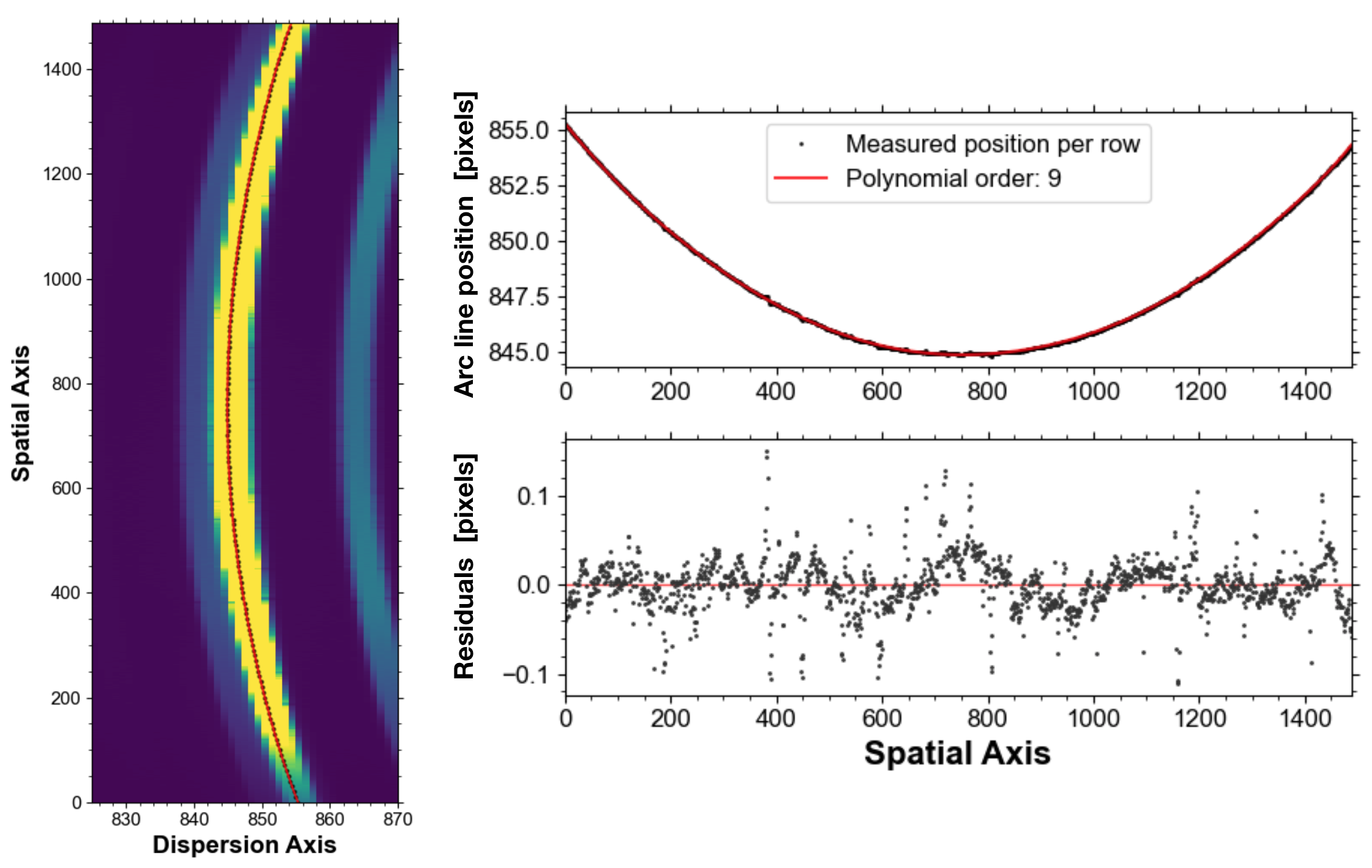
Fig. 3 – Zoom-in region around one arc line (left). The small black points indicate the fitted line position for each row (only every 5 row is shown for visual vlarity). The points have been fitted with a Chebyshev polynomium in order to obtain a smooth function shown by the red line. The top right panel shows the fitted positions of the emission line per spatial row. Black points again show the position for each row and the red line shows the fitted polynomium. The bottom right panel shows the residuals after subtracting the best-fit polonymium.

These predicted positions are obtained for each arc line in the pixel table generated by PyNOT-identify. The result after this subtask is a 2-dimensional pixel table where each identified arc line has been traced along the spatial rows. The 2D pixel table is overplotted on the trimmed arc line image and saved as a diagnostic plot. It is a good idea to inspect this plot to verify that all arc lines have been traced correctly. One example of such a 2D pixel table is shown in Fig. 4.

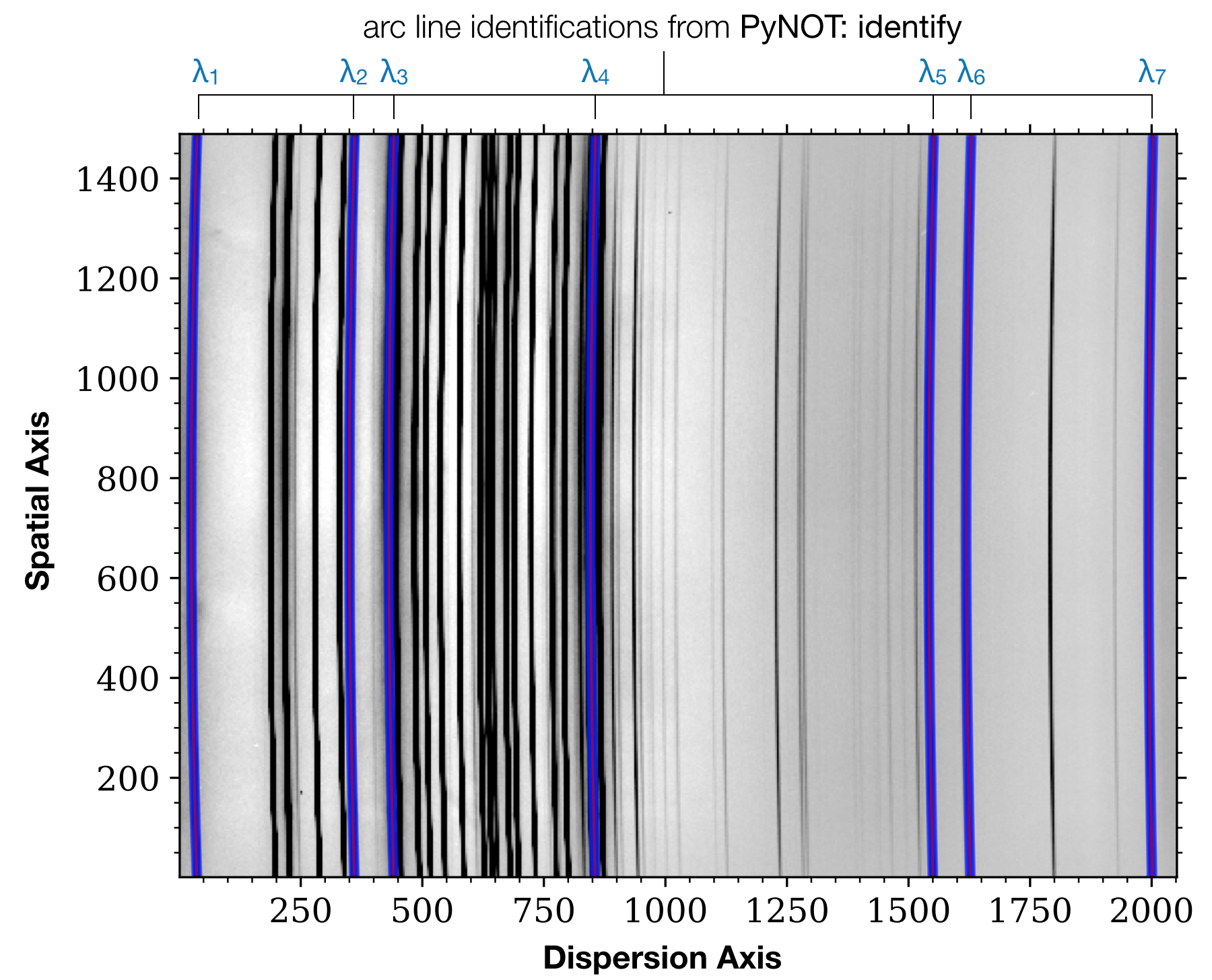
Fig. 4 – An example of the diagnostic 2D pixel table plot from PyNOT-wave2d. The input arc line image has been trimmed and rotated (gray-scale background image). Each arc line identified by the PyNOT-identify task ( λ1 , ... , λ7 ) has been traced along the spatial axis (blue points) and the best-fit predicted positions are shown as the red line.

Obs! If the input arc line image has been over- or under-exposed, the automated line tracing may fail. You should always make sure that the arc line images have been appropriately exposed. If there's a large contrast between bright and faint arc lines, or if the illumination towards the slit edge is too poor, it might be necessary to combine several arc line images taken with the same slit.

Image transformation and wavelength linearization

The wavelength solution at each spatial row is then obtained as: ​ \( \lambda_i (x) = C_{\tt order\_wl}(x\ |\ \lambda_{\mathrm{ref}}, x_{{\rm ref}, i}) \) where \(C_{\tt order\_wl}\) refers to a Chebyshev polynomium of order determined by the parameter order_wl, given the interpolation reference wavelengths, \(\lambda_{\rm ref}\) and the arc line position for the given row, \(x_{{\rm ref}, i}\) (see above). In order to rectify the science frame, each row along with its associated error and quality mask is now interpolated onto the reference wavelength grid. The central row is by default assumed as the reference position. Hence, all other rows will be aligned to the wavelengths defined by the central row (or whatever row was used to identify the arc lines). Values that fall outside the reference wavelength grid are set to 0.

Example Syntax

pynot wave2d --table TABLE -o OUTPUT input arc


Full example of command line syntax:

pynot wave2d [-h] --table TABLE -o OUTPUT [--axis AXIS] [--order_wl ORDER_WL] [--order_bg ORDER_BG] [--order_2d ORDER_2D] [--log LOG] [--N_out N_OUT] [--interpolate INTERPOLATE] [--fit_window FIT_WINDOW] [--plot PLOT] [--edge_kappa EDGE_KAPPA] input arc



Overview of parameters

input
Input filename of 2D spectrum
arc
Input filename of arc line image
--table
Pixeltable of line identification from 'PyNOT-identify' [REQUIRED]
--output (-o)
Output filename of rectified, wavelength calibrated 2D image [REQUIRED]
Optional Arguments:
--axis: 2
Dispersion axis: 1 horizontal, 2: vertical
--order_wl: 5
Order of Chebyshev polynomium for wavelength solution
--order_bg: 5
Polynomial order for background subtraction of calibration lamp continuum
--order_2d: 3
Polynomial order for spatial reconstruction of arc lines
--log: False
Use logarithmic binning in wavelength?
--N_out: None
No. of output pixels along dispersion axis. If null is given, use No. of pixels in input image.
--interpolate: True
Perform interpolation or apply central wavelength solution to full 2D range
--fit_window: 10
Fitting window in pixels around each arc line to determine centroid (optimized for grism 4)
--plot: True
Make diagnostic plots?
--edge_kappa: 10
Significance threshold for edge detection of arc lines